mod_fem_viewer/FemViewer/src/elem_tables.cpp File Reference

#include "Enums.h"
#include "elem_tables.h"
#include "Point3D.h"
#include <stdio.h>
#include <iostream>
#include <algorithm>
#include <map>
#include <assert.h>
#include <string.h>
Include dependency graph for elem_tables.cpp:

Defines

#define X   -1

Typedefs

typedef unsigned int indextype

Functions

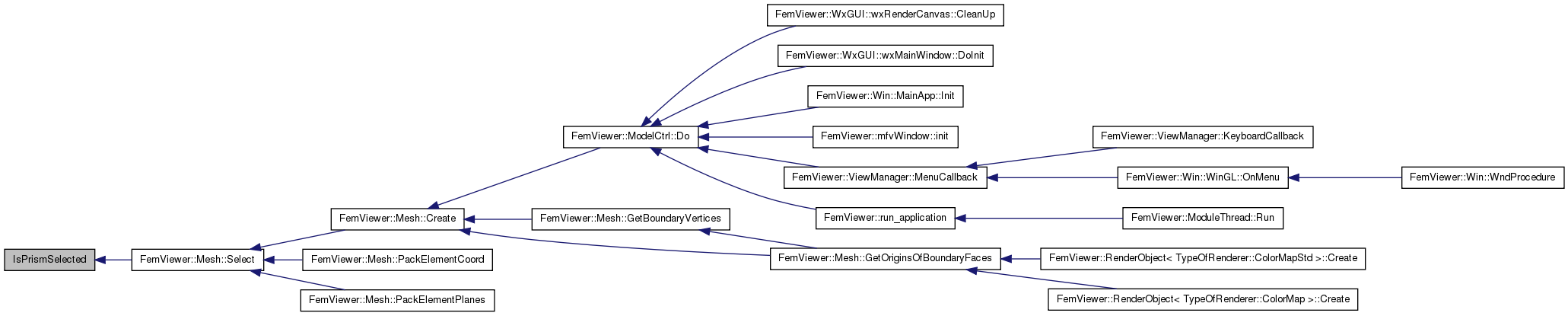
int IsPrismSelected (const double coords[6 *4], const double *plane)
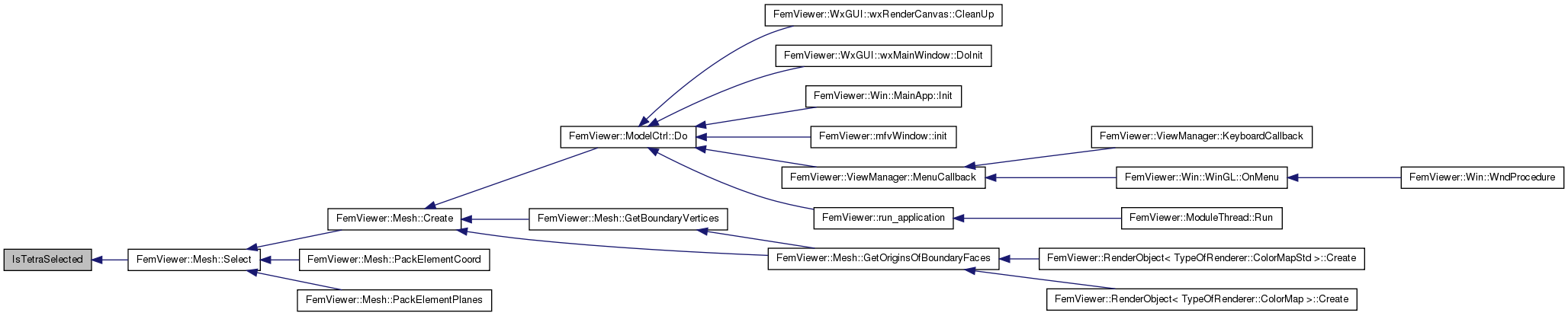
int IsTetraSelected (const double coords[4 *4], const double *plane)
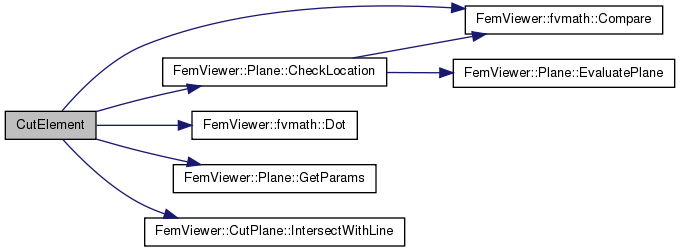
unsigned int CutElement (const double vertices[18], const int nodes[7], const myPlane *cut_plane, std::vector< myVertex > &out_vertices)
bool getSimilarVertexIndex (Vertex &packed, std::map< Vertex, indextype, comp > &VertexToOutIndex, indextype &result)
void indexVBO (std::vector< Vertex > &inout_vertices, std::vector< indextype > &inout_indices)
template<typename T >
T mark_edges_in_triangle (int s, int u, const int dim)
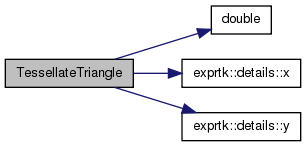
unsigned TessellateTriangle (const myVertex *a, const myVertex *b, const myVertex *c, int ndiv, std::vector< myVertex > &vertices, std::vector< unsigned > &indices)

Variables

const int iTetraEdgeConnect [6][2]
const int iTetraVertcesOfEdges [4][3]
int iTetraEdgeTbl [16]
int iTetrahedronTrianglesCT [16][7]
int iSideTrainglesCT [16][4][6]
const int iPrismEdges [9][2]
const int iPrismVerticesOfEdges [6][3]
const int iPrismEdgesOfFaces [9][2]
int iQuadEdgesIds [4][2]
int iSLinesCT [16][5]
int iQuadFlags [16]
int iQuadEdges [16][7]
const int iPrismFaces [5][4] = {{0,2,1,-1},{3,4,5,-1},{0,1,4,3},{1,2,5,4},{0,3,5,2}}
const int iPrizmMidPts [5][4] = {{6,7,8,-1},{9,10,11,-1},{6,13,9,12},{7,14,10,13},{8,12,11,14}}

Define Documentation

#define X   -1

Typedef Documentation

typedef unsigned int indextype

Function Documentation

unsigned int CutElement ( const double  vertices[18],
const int  nodes[7],
const myPlane *  cut_plane,
std::vector< myVertex > &  out_vertices 
)

Here is the call graph for this function:

Here is the caller graph for this function:

bool getSimilarVertexIndex ( Vertex &  packed,
std::map< Vertex, indextype, comp > &  VertexToOutIndex,
indextype &  result 
)

Here is the caller graph for this function:

void indexVBO ( std::vector< Vertex > &  inout_vertices,
std::vector< indextype > &  inout_indices 
)

Here is the call graph for this function:

int IsPrismSelected ( const double  coords[6 *4],
const double *  plane 
)

Here is the caller graph for this function:

int IsTetraSelected ( const double  coords[4 *4],
const double *  plane 
)

Here is the caller graph for this function:

template<typename T >
T mark_edges_in_triangle ( int  s,
int  u,
const int  dim 
) [inline]
unsigned TessellateTriangle ( const myVertex *  a,
const myVertex *  b,
const myVertex *  c,
int  ndiv,
std::vector< myVertex > &  vertices,
std::vector< unsigned > &  indices 
)

Here is the call graph for this function:

Here is the caller graph for this function:

Variable Documentation

const int iPrismEdges[9][2]
Initial value:
 {
    { 0, 1 },
    { 1, 2 },
    { 0, 2 },
    { 3, 4 },
    { 4, 5 },
    { 3, 5 },
    { 0, 3 },
    { 1, 4 },
    { 2, 5 }
}
const int iPrismEdgesOfFaces[9][2]
Initial value:
 {
    {0,2}, {0,3}, {0,4}, {1,2}, {1,3}, {1,4}, {2,4}, {2,3}, {3,4}
}
const int iPrismFaces[5][4] = {{0,2,1,-1},{3,4,5,-1},{0,1,4,3},{1,2,5,4},{0,3,5,2}}
const int iPrismVerticesOfEdges[6][3]
Initial value:
 {
    {0,2,6}, {0,1,7}, {1,2,8}, {3,5,6}, {3,4,7}, {4,5,8}
}
const int iPrizmMidPts[5][4] = {{6,7,8,-1},{9,10,11,-1},{6,13,9,12},{7,14,10,13},{8,12,11,14}}
int iQuadEdges[16][7]
Initial value:
 {
    {0,-1,-1,-1,-1,-1,-1}, 
    {3, 0, 4, 7,-1,-1,-1}, 
    {3, 1, 5, 4,-1,-1,-1}, 
    {4, 0, 1, 5, 7,-1,-1}, 
    {3, 2, 6, 5,-1,-1,-1}, 
    {6, 0, 4, 7, 2, 6, 5}, 
    {4, 1, 2, 6, 4,-1,-1}, 
    {5, 0, 1, 2, 6, 7,-1}, 
    {3, 3, 7, 6,-1,-1,-1}, 
    {4, 0, 4, 6, 3,-1,-1}, 
    {6, 1, 5, 4, 3, 7, 6}, 
    {5, 0, 1, 5, 6, 3,-1}, 
    {4, 2, 3, 7, 5,-1,-1}, 
    {5, 0, 4, 5, 2, 3,-1}, 
    {5, 1, 2, 3, 7, 4,-1}, 
    {4, 0, 1, 2, 3,-1,-1}, 
}
int iQuadEdgesIds[4][2]
Initial value:
 {
    {0,1},{1,2},{2,3},{3,0}
}
int iQuadFlags[16]
Initial value:
 {
    0x00,
    0x09,
    0x03,
    0x0a,
    0x06,
    0x0f,
    0x05,
    0x0c,
    0x0c,
    0x05,
    0x0f,
    0x06,
    0x0a,
    0x03,
    0x09,
    0x00
}
int iSideTrainglesCT[16][4][6]
Initial value:
 
{
    { {-1,-1,-1,-1,-1,-1}, {-1,-1,-1,-1,-1,-1}, {-1,-1,-1,-1,-1,-1}, {-1,-1,-1,-1,-1,-1} }, 
    { { 0, 6, 4,-1,-1,-1}, { 0, 4, 7,-1,-1,-1}, { 0, 7, 6,-1,-1,-1}, {-1,-1,-1,-1,-1,-1} }, 
    { { 1, 4, 5,-1,-1,-1}, { 8, 4, 1,-1,-1,-1}, {-1,-1,-1,-1,-1,-1}, { 1, 5, 8,-1,-1,-1} }, 
    { { 6, 5, 1, 6, 1, 0}, { 8, 7, 0, 8, 0, 1}, { 7, 6, 0,-1,-1,-1}, { 1, 5, 8,-1,-1,-1} }, 
    { { 2, 5, 6,-1,-1,-1}, {-1,-1,-1,-1,-1,-1}, { 2, 6, 9,-1,-1,-1}, { 9, 5, 2,-1,-1,-1} }, 
    { { 0, 2, 5, 0, 5, 4}, { 0, 4, 7,-1,-1,-1}, { 7, 9, 2, 7, 2, 0}, { 2, 9, 5,-1,-1,-1} }, 
    { { 6, 2, 1, 6, 1, 4}, { 8, 4, 1,-1,-1,-1}, { 2, 6, 9,-1,-1,-1}, { 8, 1, 2, 8, 2, 9} }, 
    { { 0, 2, 1,-1,-1,-1}, { 7, 0, 1, 7, 1, 8}, { 0, 7, 9, 0, 9, 2}, { 8, 1, 2, 8, 2, 9} }, 
    { {-1,-1,-1,-1,-1,-1}, { 3, 7, 8,-1,-1,-1}, { 9, 7, 3,-1,-1,-1}, { 3, 8, 9,-1,-1,-1} }, 
    { { 6, 4, 0,-1,-1,-1}, { 4, 8, 3, 4, 3, 0}, { 9, 6, 0, 9, 0, 3}, { 3, 8, 9,-1,-1,-1} }, 
    { { 1, 4, 5,-1,-1,-1}, { 1, 3, 7, 1, 7, 4}, { 9, 7, 3,-1,-1,-1}, { 5, 9, 3, 5, 3, 1} }, 
    { { 6, 5, 1, 6, 1, 0}, { 0, 1, 3,-1,-1,-1}, { 0, 3, 9, 0, 9, 6}, { 5, 9, 3, 5, 3, 1} }, 
    { { 2, 5, 6,-1,-1,-1}, { 3, 7, 8,-1,-1,-1}, { 6, 7, 3, 6, 3, 2}, { 2, 3, 8, 2, 8, 5} }, 
    { { 5, 4, 0, 5, 0, 2}, { 4, 8, 3, 4, 3, 0}, { 0, 3, 2,-1,-1,-1}, { 2, 3, 8, 2, 8, 5} }, 
    { { 4, 6, 2, 4, 2, 1}, { 1, 3, 7, 1, 7, 4}, { 6, 7, 3, 6, 3, 2}, { 1, 2, 3,-1,-1,-1} }, 
    { { 0, 2, 1,-1,-1,-1}, { 0, 1, 3,-1,-1,-1}, { 0, 3, 2,-1,-1,-1}, { 1, 2, 3,-1,-1,-1} }  
}
int iSLinesCT[16][5]
Initial value:
  {
    {-1, -1, -1, -1, -1},
    {0, 3, -1, -1, -1},
    {0, 1, -1, -1, -1},
    {3, 1, -1, -1, -1},
    {2, 1, -1, -1, -1},
    {0, 1,  3,  2, -1}, 
    {2, 0, -1, -1, -1},
    {2, 3, -1, -1, -1},
    {2, 3, -1, -1, -1},
    {2, 0, -1, -1, -1},
    {1, 0,  3,  2, -1}, 
    {2, 1, -1, -1, -1},
    {3, 1, -1, -1, -1},
    {0, 1, -1, -1, -1},
    {3, 0, -1, -1, -1},
    {-1, -1, -1, -1, -1}
  }
const int iTetraEdgeConnect[6][2]
Initial value:
 {
    {0,1}, {1,2}, {0,2}, {0,3}, {1,3}, {2,3}
}
int iTetraEdgeTbl[16]
Initial value:
  {
    0x000, 
    0x00d, 
    0x013, 
    0x01e, 
    0x026, 
    0x02b, 
    0x035, 
    0x038, 
    0x038, 
    0x035, 
    0x02b, 
    0x026, 
    0x01e, 
    0x013, 
    0x00d, 
    0x000, 
  }
int iTetrahedronTrianglesCT[16][7]
Initial value:
  {
    {-1, -1, -1, -1, -1, -1, -1}, 
    { 0,  3,  2, -1, -1, -1, -1}, 
    { 0,  1,  4, -1, -1, -1, -1}, 
    { 1,  4,  3,  1,  3,  2, -1}, 

    { 1,  2,  5, -1, -1, -1, -1}, 
    { 0,  3,  5,  0,  5,  1, -1}, 
    { 0,  2,  5,  0,  5,  4, -1}, 
    { 5,  4,  3, -1, -1, -1, -1}, 

    { 3,  4,  5, -1, -1, -1, -1}, 
    { 4,  5,  0,  5,  2,  0, -1}, 
    { 1,  5,  0,  5,  3,  0, -1}, 
    { 5,  2,  1, -1, -1, -1, -1}, 

    { 2,  3,  1,  3,  4,  1, -1}, 
    { 4,  1,  0, -1, -1, -1, -1}, 
    { 2,  3,  0, -1, -1, -1, -1}, 
    {-1, -1, -1, -1, -1, -1, -1}, 
  }
const int iTetraVertcesOfEdges[4][3]
Initial value:
 { 
    {0,1,2}, {0,1,3}, {0,2,3}, {1,2,3}
}
 All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Defines
Generated on 3 Jun 2020 for ModFEM by  doxygen 1.6.1