lsd_mkb/lsd_mkb_superlu/superlu_seq/dlamch.c File Reference

#include <stdio.h>
#include "slu_Cnames.h"

Include dependency graph for dlamch.c:

Defines
#define	TRUE_   (1)
#define	FALSE_   (0)
#define	abs(x)   ((x) >= 0 ? (x) : -(x))
#define	min(a, b)   ((a) <= (b) ? (a) : (b))
#define	max(a, b)   ((a) >= (b) ? (a) : (b))
Functions
double	dlamch_ (char *cmach)
int	dlamc1_ (int *beta, int *t, int *rnd, int *ieee1)
int	dlamc2_ (int *beta, int *t, int *rnd, double *eps, int *emin, double *rmin, int *emax, double *rmax)
double	dlamc3_ (double *a, double *b)
int	dlamc4_ (int *emin, double *start, int *base)
int	dlamc5_ (int *beta, int *p, int *emin, int *ieee, int *emax, double *rmax)
double	pow_di (double *ap, int *bp)

---

Define Documentation

#define abs

(

x

)

((x) >= 0 ? (x) : -(x))

#define FALSE_   (0)

#define max	(	a,
		b		)	((a) >= (b) ? (a) : (b))

#define min	(	a,
		b		)	((a) <= (b) ? (a) : (b))

#define TRUE_   (1)

---

Function Documentation

int dlamc1_	(	int *	beta,
		int *	t,
		int *	rnd,
		int *	ieee1
	)

 Purpose   
    =======

    DLAMC1 determines the machine parameters given by BETA, T, RND, and   
    IEEE1.

    Arguments   
    =========

    BETA    (output) INT   
            The base of the machine.

    T       (output) INT   
            The number of ( BETA ) digits in the mantissa.

    RND     (output) INT   
            Specifies whether proper rounding  ( RND = .TRUE. )  or   
            chopping  ( RND = .FALSE. )  occurs in addition. This may not

            be a reliable guide to the way in which the machine performs

            its arithmetic.

    IEEE1   (output) INT   
            Specifies whether rounding appears to be done in the IEEE   
            'round to nearest' style.

    Further Details   
    ===============

    The routine is based on the routine  ENVRON  by Malcolm and   
    incorporates suggestions by Gentleman and Marovich. See

       Malcolm M. A. (1972) Algorithms to reveal properties of   
          floating-point arithmetic. Comms. of the ACM, 15, 949-951.

       Gentleman W. M. and Marovich S. B. (1974) More on algorithms   
          that reveal properties of floating point arithmetic units.   
          Comms. of the ACM, 17, 276-277.

   ===================================================================== 

Here is the call graph for this function:

Here is the caller graph for this function:

int dlamc2_	(	int *	beta,
		int *	t,
		int *	rnd,
		double *	eps,
		int *	emin,
		double *	rmin,
		int *	emax,
		double *	rmax
	)

    Purpose   
    =======

    DLAMC2 determines the machine parameters specified in its argument   
    list.

    Arguments   
    =========

    BETA    (output) INT   
            The base of the machine.

    T       (output) INT   
            The number of ( BETA ) digits in the mantissa.

    RND     (output) INT   
            Specifies whether proper rounding  ( RND = .TRUE. )  or   
            chopping  ( RND = .FALSE. )  occurs in addition. This may not

            be a reliable guide to the way in which the machine performs

            its arithmetic.

    EPS     (output) DOUBLE PRECISION   
            The smallest positive number such that

               fl( 1.0 - EPS ) .LT. 1.0,

            where fl denotes the computed value.

    EMIN    (output) INT   
            The minimum exponent before (gradual) underflow occurs.

    RMIN    (output) DOUBLE PRECISION   
            The smallest normalized number for the machine, given by   
            BASE**( EMIN - 1 ), where  BASE  is the floating point value

            of BETA.

    EMAX    (output) INT   
            The maximum exponent before overflow occurs.

    RMAX    (output) DOUBLE PRECISION   
            The largest positive number for the machine, given by   
            BASE**EMAX * ( 1 - EPS ), where  BASE  is the floating point

            value of BETA.

    Further Details   
    ===============

    The computation of  EPS  is based on a routine PARANOIA by   
    W. Kahan of the University of California at Berkeley.

   ===================================================================== 

Here is the call graph for this function:

Here is the caller graph for this function:

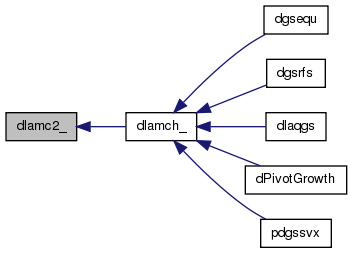
double dlamc3_	(	double *	a,
		double *	b
	)

    Purpose   
    =======

    DLAMC3  is intended to force  A  and  B  to be stored prior to doing

    the addition of  A  and  B ,  for use in situations where optimizers

    might hold one of these in a register.

    Arguments   
    =========

    A, B    (input) DOUBLE PRECISION   
            The values A and B.

   ===================================================================== 

Here is the caller graph for this function:

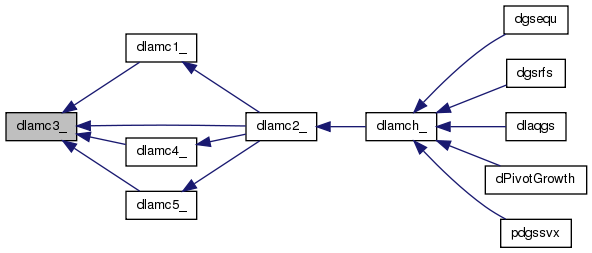
int dlamc4_	(	int *	emin,
		double *	start,
		int *	base
	)

    Purpose   
    =======

    DLAMC4 is a service routine for DLAMC2.

    Arguments   
    =========

    EMIN    (output) EMIN   
            The minimum exponent before (gradual) underflow, computed by

            setting A = START and dividing by BASE until the previous A   
            can not be recovered.

    START   (input) DOUBLE PRECISION   
            The starting point for determining EMIN.

    BASE    (input) INT   
            The base of the machine.

   ===================================================================== 

Here is the call graph for this function:

Here is the caller graph for this function:

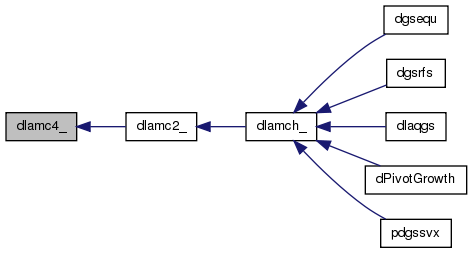
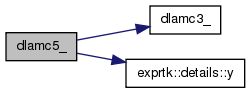
int dlamc5_	(	int *	beta,
		int *	p,
		int *	emin,
		int *	ieee,
		int *	emax,
		double *	rmax
	)

    Purpose   
    =======

    DLAMC5 attempts to compute RMAX, the largest machine floating-point   
    number, without overflow.  It assumes that EMAX + abs(EMIN) sum   
    approximately to a power of 2.  It will fail on machines where this   
    assumption does not hold, for example, the Cyber 205 (EMIN = -28625,

    EMAX = 28718).  It will also fail if the value supplied for EMIN is   
    too large (i.e. too close to zero), probably with overflow.

    Arguments   
    =========

    BETA    (input) INT   
            The base of floating-point arithmetic.

    P       (input) INT   
            The number of base BETA digits in the mantissa of a   
            floating-point value.

    EMIN    (input) INT   
            The minimum exponent before (gradual) underflow.

    IEEE    (input) INT   
            A int flag specifying whether or not the arithmetic   
            system is thought to comply with the IEEE standard.

    EMAX    (output) INT   
            The largest exponent before overflow

    RMAX    (output) DOUBLE PRECISION   
            The largest machine floating-point number.

   =====================================================================

       First compute LEXP and UEXP, two powers of 2 that bound   
       abs(EMIN). We then assume that EMAX + abs(EMIN) will sum   
       approximately to the bound that is closest to abs(EMIN).   
       (EMAX is the exponent of the required number RMAX).

Here is the call graph for this function:

Here is the caller graph for this function:

double dlamch_

(

char *

cmach

)

    Purpose   
    =======

    DLAMCH determines double precision machine parameters.

    Arguments   
    =========

    CMACH   (input) CHARACTER*1   
            Specifies the value to be returned by DLAMCH:   
            = 'E' or 'e',   DLAMCH := eps   
            = 'S' or 's ,   DLAMCH := sfmin   
            = 'B' or 'b',   DLAMCH := base   
            = 'P' or 'p',   DLAMCH := eps*base   
            = 'N' or 'n',   DLAMCH := t   
            = 'R' or 'r',   DLAMCH := rnd   
            = 'M' or 'm',   DLAMCH := emin   
            = 'U' or 'u',   DLAMCH := rmin   
            = 'L' or 'l',   DLAMCH := emax   
            = 'O' or 'o',   DLAMCH := rmax

            where

            eps   = relative machine precision   
            sfmin = safe minimum, such that 1/sfmin does not overflow   
            base  = base of the machine   
            prec  = eps*base   
            t     = number of (base) digits in the mantissa   
            rnd   = 1.0 when rounding occurs in addition, 0.0 otherwise   
            emin  = minimum exponent before (gradual) underflow   
            rmin  = underflow threshold - base**(emin-1)   
            emax  = largest exponent before overflow   
            rmax  = overflow threshold  - (base**emax)*(1-eps)

   ===================================================================== 

Here is the caller graph for this function:

double pow_di	(	double *	ap,
		int *	bp
	)

Here is the call graph for this function:

Here is the caller graph for this function: